
A buen seguro conocerás en qué consiste el código binario, fundamental a la hora de comunicarnos con las máquinas. Sin embargo, puede que no conozcas que también existe un alfabeto binario que traduce todas las letras a este sistema. Te lo explicamos a continuación.
Índice
- Qué es el código binario
- Qué es el alfabeto binario
- Cómo traducir de binario a texto
- Cómo convertir un texto en binario
Qué es el código binario
La mayoría de la gente usa el conocido como sistema decimal, que está compuesto por diez cifras que van del cero al nueve. Para representar números más altos vamos añadiendo posiciones a la izquierda de esta cifra.
El sistema binario funciona de una forma parecida, pero utilizando solo dos dígitos, en vez de diez, que pueden ser un cero o un uno. Este sistema de codificación supone una abstracción perfecta de un estado eléctrico de encendido o apagado. Es decir, que lo podemos representar como ‘verdadero’ o ‘falso’ según circule o no el voltaje. Esta es la razón por la cual el código binario se emplea de manera prioritaria a nivel de lenguaje máquina y por la que resulta importante conocer cómo funciona.
En el código binario, cada posición de un dígito representará una potencia de 2. Para quienes tengan nociones de informática y computación, es un conocimiento tan prioritario como el del código ASCII. Aunque hay otras asociaciones como la del braille, el sistema de lectura y escritura táctil para personas con discapacidad visual, que extrapola este sistema binario a una matriz de seis puntos.
Qué es el alfabeto binario
El braille, de hecho, es un buen ejemplo de las posibilidades de un sistema binario extendido. Utilizando este código se pueden representar nuestras letras, incluyendo mayúsculas y minúsculas. Con siete posiciones a elegir entre ceros y unos podríamos abarcar todo el alfabeto, y habría que irse a ocho para añadir las vocales con tilde. A continuación, las dos tablas.
Letras mayúsculas del alfabeto binario
| A | 01000001 |
| Á | 11000001 |
| B | 01000010 |
| C | 01000011 |
| D | 01000100 |
| E | 01000101 |
| É | 11001001 |
| F | 01000110 |
| G | 01000111 |
| H | 01001000 |
| I | 01001001 |
| Í | 11001101 |
| J | 01001010 |
| K | 01001011 |
| L | 01001100 |
| M | 01001101 |
| N | 01001110 |
| Ñ | 11010001 |
| O | 01001111 |
| Ó | 11010011 |
| P | 01010000 |
| Q | 01010001 |
| R | 01010010 |
| S | 01010011 |
| T | 01010100 |
| U | 01010101 |
| Ú | 11011010 |
| Ü | 11011100 |
| V | 01010110 |
| W | 01010111 |
| X | 01011000 |
| Y | 01011001 |
| Z | 01011010 |
Letras minúsculas del alfabeto binario
| a | 01100001 |
| á | 11100001 |
| b | 01100010 |
| c | 01100011 |
| d | 01100100 |
| e | 01100101 |
| é | 11101001 |
| f | 01100110 |
| g | 01100111 |
| h | 01101000 |
| i | 01101001 |
| í | 11101101 |
| j | 01101010 |
| k | 01101011 |
| l | 01101100 |
| m | 01101101 |
| n | 01101110 |
| ñ | 11110001 |
| o | 01101111 |
| ó | 11110011 |
| p | 01110000 |
| q | 01110001 |
| r | 01110010 |
| s | 01110011 |
| t | 01110100 |
| u | 01110101 |
| ú | 11111010 |
| ü | 11111100 |
| v | 01110110 |
| w | 01110111 |
| x | 01111000 |
| y | 01111001 |
| z | 01111010 |
Cómo traducir de binario a texto
Tanto si se trabaja de manera habitual en proyectos informáticos como por pura curiosidad, existen maneras de traducir de alfabeto binario a texto. ¿Cómo se hace? Hay que ayudarse de una tabla en la cual se van asociando números, desde el 65 al 122, a las letras del alfabeto, empezando por las mayúsculas.
A continuación se multiplicarían las posiciones de ceros o unos por sus potencias respectivas de dos y de la suma de esas cuentas se obtendría la letra representada. Como puede parecer más complicado de lo que es, a continuación enlazamos con una explicación visual, muy sencilla, de cómo funcionaría este proceso.
De todas formas, como a día de hoy resulta muy raro que no llevemos siempre encima un dispositivo ‘inteligente’, lo más práctico es hacer uso de alguno de los muchos convertidores disponibles. Algunos de los traductores de binario a texto más populares son Convert Binary, Traductor Binario o RapidTables, aunque las opciones son diversas.
Cómo convertir un texto en binario
También es interesante conocer cómo funciona la traducción inversa, es decir, convertir un texto en binario. Para ello debemos apoyarnos de nuevo en la tabla de asociaciones entre letras y números de la cual hablamos antes. Para representar cada letra del alfabeto empezaríamos a dividir su número entre dos, y ese resultado entre dos, de manera recursiva.
El ‘truco’ está en ir anotando si los restos de estas divisiones son ceros o unos, lo que nos dará la solución. Al igual que en el apartado anterior, es útil y esclarecedor ver este proceso de una manera visual. Así se entenderá mejor cómo se calculan las secuencias binarias de cada letra, hasta completar la palabra buscada.
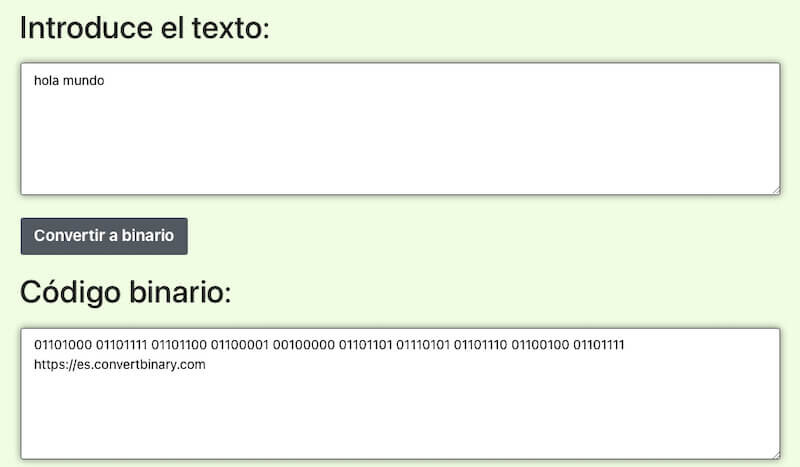
Como es una cuenta un poco farragosa, lo más lógico será acudir a la tabla de equivalencias del segundo punto. O también, utilizar los convertidores online para que hagan el ‘trabajo sucio’. Las mismas plataformas citadas anteriormente, como Convert Binary y Traductor Binario, además de otras como Calculatored, también codifican a la inversa, además de a otros sistemas como el decimal o el hexadecimal.
En Nobbot | Grace Hopper, la anónima creadora del compilador de lenguaje que avanzó la programación
Imágenes | Portada: foto de Alexander Sinnh en Unsplash. Interiores: vídeo del canal PrograMate, vídeo del canal Pasos por Ingeniería y pantallazo del traductor ConverBinary.


