A lo largo de nuestra formación académica aprendemos un sinfín de conocimientos. Algunos permanecen en nuestra memoria, pero otros no. Si ahora te preguntan qué es un triángulo equilátero y cómo calcular su área y perímetro, ¿sabrías hacerlo?
Índice
- Definición, elementos y propiedades del triángulo equilátero
- Fórmulas del triángulo equilátero: cómo calcularla el perímetro, el área y más
- Ejemplos resueltos de problemas de triángulos equiláteros
Definición, elementos y propiedades del triángulo equilátero
El estudio de los triángulos equiláteros se encuadra dentro de la geometría, que es la parte de las matemáticas que indaga y profundiza en las propiedades que tienen las figuras en el espacio y sobre plano. La característica singular de este polígono regular es que sus tres lados son iguales. También sus ángulos internos, de ahí que sea posible referirse a ellos también con el nombre de equiangulares.
Está formado por diferentes elementos y algunos de los más importantes son:
- Vértice: es el punto donde coinciden los dos lados de un ángulo. En la imagen se corresponde con las letras A, B y C.
- Lados: son las líneas que conforman el triángulo. En el ejemplo: AB, AC y BC. Todos miden lo mismo. En el ejemplo de la imagen, cada lado posee una longitud de 15 cm.
- Ángulos interiores: esta clase de ángulos está formado por los dos lados del triángulo que comparten un vértice común. Se encuentran dentro del propio triángulo. En los equiláteros, la suma de estos tres ángulos interiores (números 1, 2 y 3) siempre da como resultado 180º porque cada ángulo mide 60º. En este vídeo podéis consultar una explicación más detallada.
- Ángulos exteriores: a diferencia de los ángulos internos, los externos (números 4, 5 y 6) se forman fuera del triángulo porque cada uno es suplementario al ángulo interior del mismo lado.
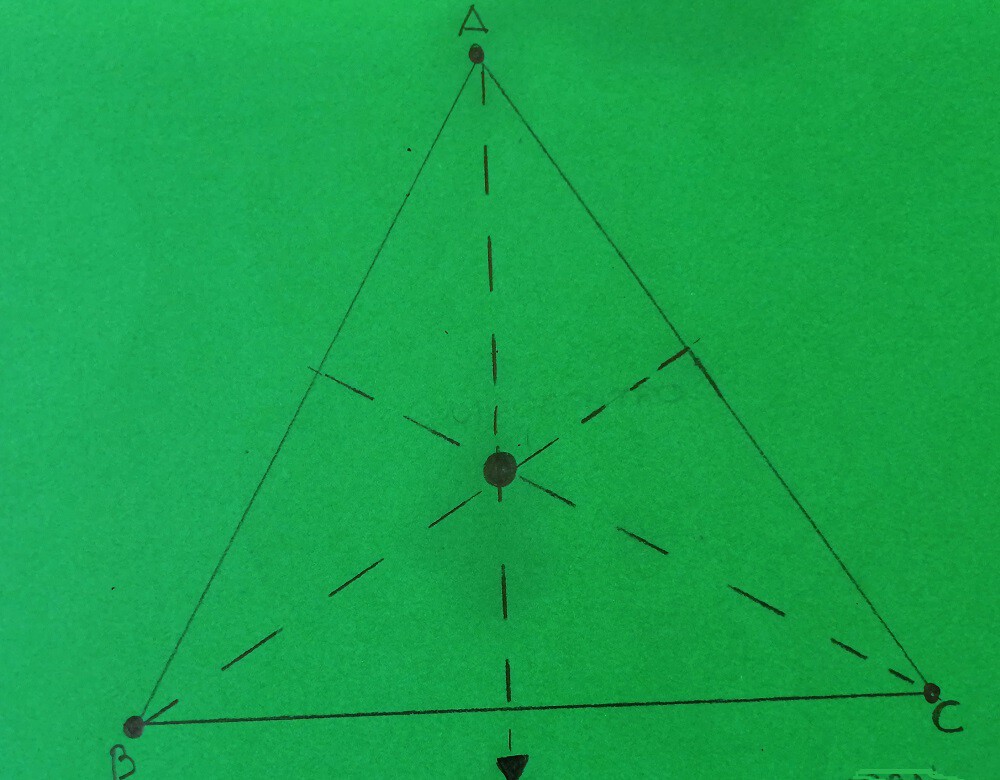
- Altura: cada segmento que une un vértice con un punto que puede ser de su lado opuesto o prolongación. Donde se cruzan o cortan las tres alturas se llama ortocentro.
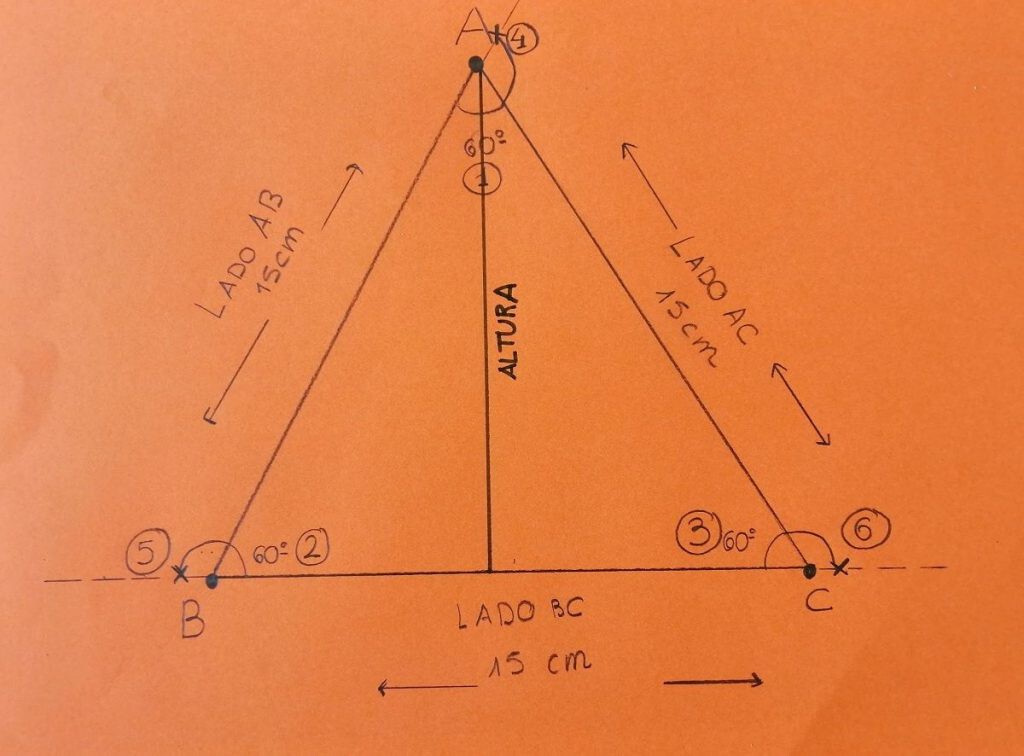
- Bisectriz: se refiere a cada una de las semirrectas de los ángulos. Su origen es el vértice del ángulo y el resultado son dos ángulos que miden lo mismo. El punto donde las tres bisectrices se juntan es el incentro.
- Mediana: recta que inicia su recorrido desde el punto medio de un lado y finaliza en el vértice contrario. El baricentro es el espacio donde las tres medianas del triángulo equilátero se ‘fusionan’.
- Eje de simetría: es la línea que divide el triángulo en dos partes iguales.
Las propiedades de los triángulos equiláteros son varias. Una de las más importantes es que el incentro, el ortocentro y el baricentro se concentran en el mismo lugar.
Fórmulas del triángulo equilátero: cómo calcular el perímetro, la altura, el área y el radio de circunferencia circunscrita
Cuando hablamos de triángulos equiláteros es habitual hacer referencia a conceptos como el perímetro, la altura o el área. Pero ¿cómo calcular estas fórmulas?
Perímetro
Es una de las fórmulas más fáciles de aplicar. Para calcular el perímetro del triángulo equilátero, debes sumar lo que miden sus tres lados. Por ejemplo, si cada lado de un triángulo equilátero mide 15 cm, el perímetro será de 45 cm (15 + 15 + 15).
Altura
Lo más sencillo es aplicar el Teorema de Pitágoras que dice lo siguiente: el cuadrado de la hipotenusa (lado opuesto al ángulo recto en un triángulo rectángulo) es igual a la suma de los cuadrados de los catetos. Imaginemos un triángulo equilátero en el que cada lado mide 16 cm. A continuación, trazamos la altura y la representamos con la letra h (así se hace en matemáticas). El resultado son dos triángulos rectángulos: sus bases miden 8 cm y uno de sus lados 16 cm. A partir de aquí, la primera operación matemática que hay que indicar una vez aplicado el citado teorema es la siguiente:
162 = h2 + 82
Ahora, resolvemos y calculamos los cuadrados: 256 = h2 + 64. A partir de aquí, el siguiente paso es:
h2 = 256 ? 64
h2 = 192
Por último, calculamos la raíz cuadrada de 192 y el resultado que se obtenga es la altura (h) del triángulo equilátero de nuestro ejemplo: 13,85.
Área
La operación matemática clásica que hay que resolver siempre y cuando sepamos los valores que necesitamos es la siguiente: base (b) por altura (h) dividido entre dos. Representada matemáticamente es (b · h) / 2.
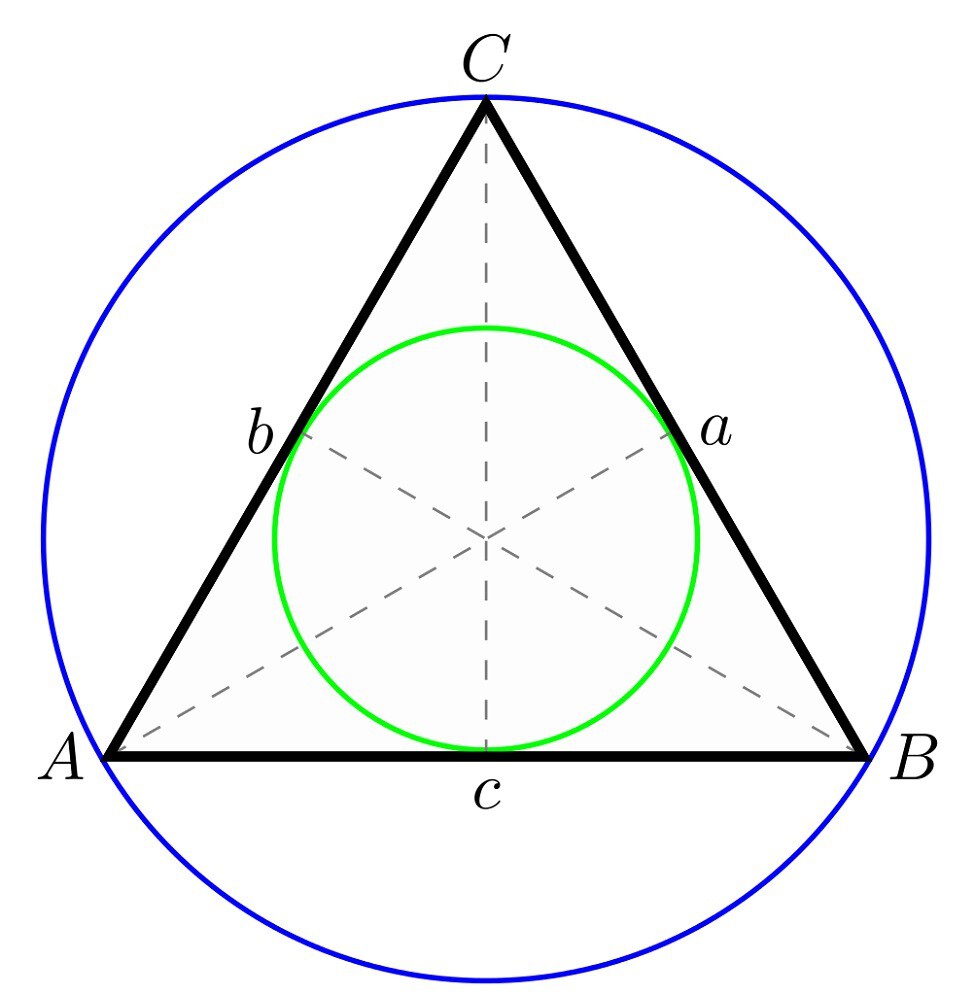
Radio de circunferencia circunscrita
Esta quizás sea la fórmula menos conocida o popular. ¿Qué es un radio de circunferencia? Es cualquier segmento que une el centro a cualquiera de los puntos de dicha circunferencia. Todos estos radios tienen en común una característica: su longitud (equivale a la mitad de lo que mide el diámetro) es la misma. En el supuesto de la circunferencia circunscrita, es decir, aquella que ‘pasa’ o toca los vértices del triángulo se calcula de la siguiente manera:
r = 2/3 de la altura (h) del triángulo equilátero
Vamos a verlo con el ejemplo que hemos desarrollado al explicar la fórmula de la altura. Como este dato ya lo tenemos, bastará con calcular los 2/3 de 13,85. Multiplicamos 13,85 por dos y el resultado (27,7) lo dividimos entre tres. El radio de la circunferencia circunscrita es 9,23.
Ejemplos resueltos de problemas de triángulos equiláteros
Una vez que hemos aprendido a identificar los elementos más importantes y fórmulas de estos polígonos regulares, vamos a resolver el siguiente problema:
¿Cómo calcular la altura de un triángulo rectángulo a partir de su área?
Tenemos un triángulo equilátero del que conocemos los siguientes datos: área 82 cm2 y base 24 cm. Como sabemos que para calcular la fórmula del área hay que usar la operación (b · h) / 2 trasladamos los valores que ya tenemos a esta:
82 cm2 = (24 · h) / 2
Para despejar h (altura) resolvemos de la siguiente manera: 82 x 2 = 24 x h
164 = 24 x h
h = 164 / 24
h = 6,83
En este enlace, tenéis otros ejercicios resueltos y para practicar.
En Nobbot | 10 maneras de aprender matemáticas sin tocar un libro
Imágenes | byMALENS/Pexels, MartinThoma/Wikimedia Commons y propias