Cómo colonizar Ceres al estilo de la serie The Expanse (y ganar espacio para la humanidad)

Si sigues la serie The Expanse, es posible que te hayas dado cuenta de las horas que echaron los guionistas y del magnífico trabajo que realizan director, actores, iluminadores y otros a la hora de reconstruir cada escena. Todo está medido al milímetro: desde la pronunciación del belter, idioma de los habitantes del Cinturón de Asteroides; hasta cómo ilumina el Sol una luna joviana o Ceres; o el serpenteo de un líquido al caer en el interior de una luna en rotación.

Tal es el cuidado casi neurótico de los guionistas de la serie, que el grueso de este artículo está enfocado a dos fotogramas dentro de una misma escena (de entre todos los fotogramas que una serie puede tener).

También es cierto que son dos fotogramas impactantes que nos muestra cómo podríamos colonizar Ceres (el planeta enano) al estilo de The Expanse, ganando así millones de hectáreas cuadradas en el Cinturón de Asteroides. El trabajo de los responsables de esta serie sus referencias sean usadas dentro de varios siglos a la hora de explorar el Sistema Solar exterior.

El metro de Ceres, planeta enano del Cinturón de Asteroides

Estos dos fotogramas aparecen en la misma escena del primer capítulo de la serie y apenas sí se les da importancia en el metraje. Muestran dos diagramas cuando uno de los protagonistas toma un vagón (similar a un coche de metro) en el interior de Ceres.

Al igual que aparece en los metros modernos de todo el mundo, en Ceres las paredes están empapeladas con mapas del metro. Aunque ellos usan pantallas en lugar de papel.

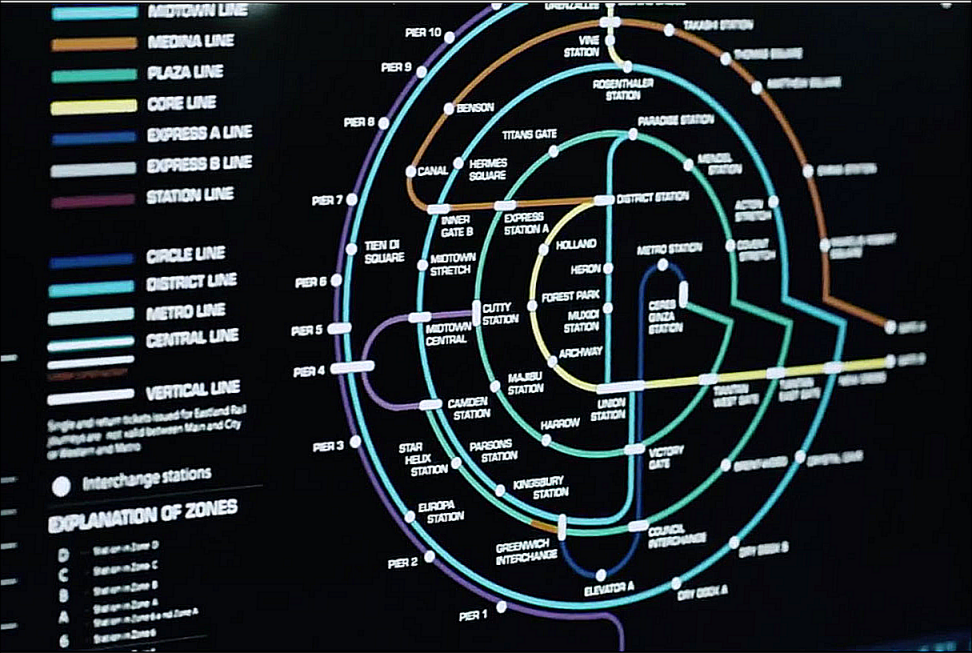
Mapa de las distintas estaciones en Ceres. Fuente:  The Expanse 1×01

En la primera de ellas se ve cómo el sistema de metro tiene una estructura de anillos concéntricos. Es la imagen de arriba, donde se leen nombres de líneas tan extraños como Línea del Núcleo o Línea Vertical.

En el fotograma de abajo se observa algo mucho más impactante que un simple plano de metro. Un plano tridimensional con las mismas líneas pero esta vez colocadas sobre una radiografía de Ceres:

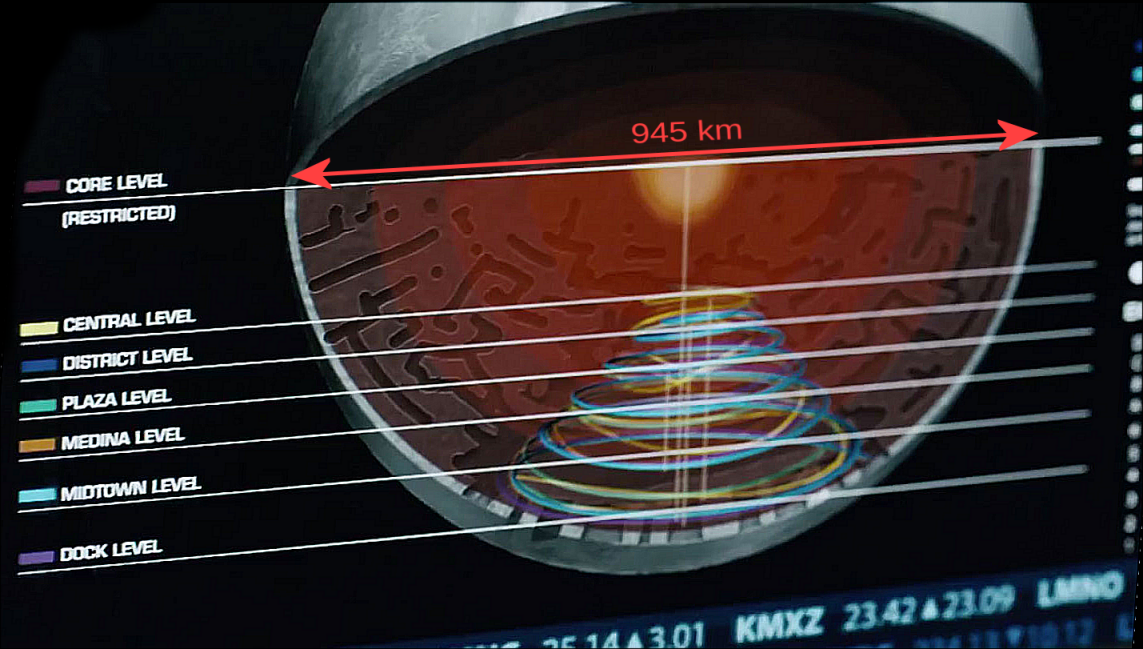
Mapa de las distintas estaciones en Ceres en 3D. Fuente:  The Expanse 1×01

Y uno puede plantearse la pregunta: ¿Por qué la estructura total tiene forma de cono o de medio diábolo? ¿Por qué los guionistas eligieron esa forma y no otra? ¿Lo hicieron al azar o esto tiene sentido a nivel físico?

Creando gravedad artificial en un planeta enano

Lo primero que hay que entender en un planeta enano como Ceres es que su gravedad no es para nada como la gravedad terrestre. Al ser más pequeño (y tener menos masa) es mucho menor.

En la superficie de Ceres existe una gravedad de 0,28 m/s² (0,029g), que difícilmente podría sostener a alguien que saltase con mucha fuerza. Es posible que en un futuro colonicemos Ceres, pero es inviable que vivamos en su superficie a largo plazo.

El motivo principal es que una gravedad tan baja como 0,28 m/s² resulta perjudicial para nuestra salud. El efecto en la salud de una gravedad baja puede verse en los astronautas que regresan tras meses en el espacio, débiles.

La gravedad en la superficie (g₀) es la mayor que existe ahora en la zona. Tanto si nos alejamos de la superficie cavando (parte izquierda de la gráfica) como si ascendemos al espacio (derecha) la gravedad disminuye.

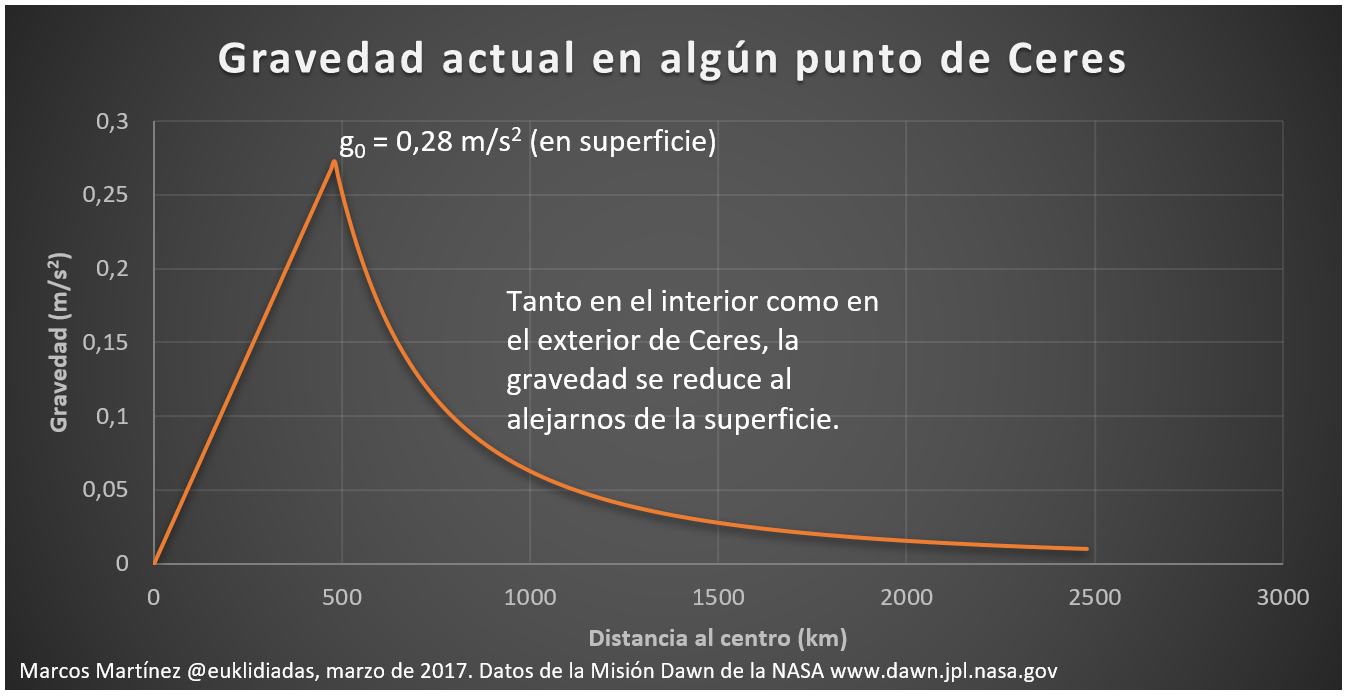
Si hemos dicho que la serie The Expanse cuida hasta los detalles más básicos, ¿por qué en la serie tienen una gravedad aceptable en el interior de Ceres?

Es porque han buscado alternativas creativas para generar gravedad en su interior usando la aceleración centrífuga.

Usando la aceleración centrífuga

La aceleración centrífuga es la misma que mantiene el agua pegada en el interior de un cubo cuando lo hacemos girar sobre nuestras cabezas. Actúa en sentido contrario al eje de giro, y crece si la velocidad de giro es elevada.

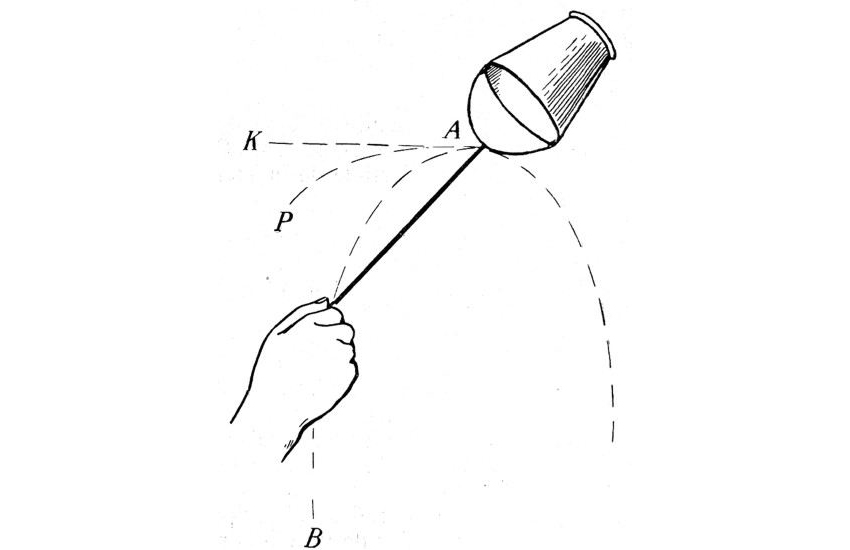
(Si no te lo crees, coge un cubo, llénalo a la mitad, y dale vueltas sobre tu cabeza. Primero rápido y luego despacio hasta que lo frenes sobre ti. Ah, y ve también a por una fregona)

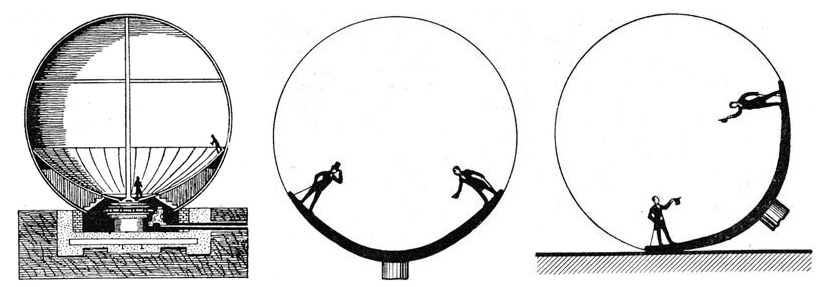
Es la misma aceleración que usaba la atracción La Esfera Encantada del siglo pasado, que giraba sobre su eje, y que hacía pensar a los incrédulos visitantes que sus iguales caminaban por la pared.

Esta misma mecánica se usa en The Expanse para hacer girar Ceres más rápido de lo que ya lo hace (ahora da una vuelta cada 9 horas) y crear así gravedad artificial en su interior.

Esto, que parece de ciencia ficción, en realidad no lo es tanto si partimos de la base de que la humanidad ha llegado al Cinturón de Asteroides y cuenta con motores que permiten hacer recorridos turísticos Tierra-Ceres a bajo coste. Aunque sí, para nuestra tecnología moderna el coste es prohibitivo.

¿Cómo funciona la gravedad artificial?

Usando un cubo o una pequeña esfera giratoria resulta sencillo usar unas fórmulas básicas para decir hemos creado X gravedad artificial. Sin embargo, cuando hablamos de planetas (inclusive planetas enanos) hay que tener en cuenta otros factores.

Como que la fuerza centrífuga va en contra de la fuerza de la gravedad en algunos puntos del planeta, pero que en otros nos ayuda con un poco de gravedad extra. (No, no es necesario seguir la nomenclatura matemática que aparece por aquí, puedes ignorarla).

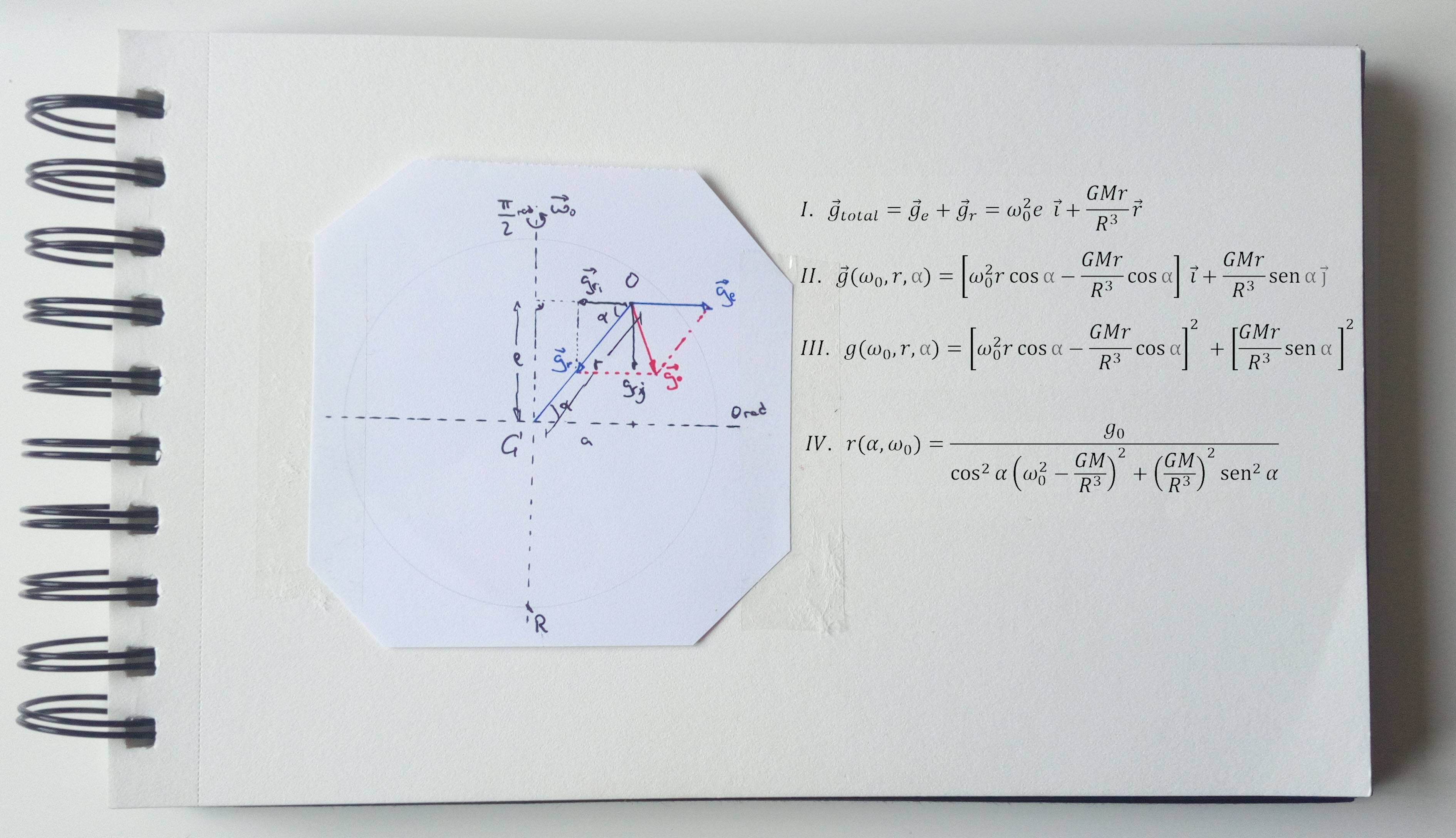
Algunas ecuaciones de un planeta en rotación. Fuente: Marcos Martínez.

En esencia, cuando se aumenta la velocidad angular (?₀) –es así como se dice que gira más rápido– de un planeta como Ceres, crece la aceleración centrífuga (?²·r) en función de cómo de lejos estemos del eje (a).

Cuanto más lejos del eje, más gravedad artificial.

¿Cuánta velocidad angular necesita Ceres?

Una de las primeras preguntas que se harían los ingenieros cinturinos es ¿Cuánta velocidad de giro necesitamos? Por supuesto, la respuesta es que depende. Depende de lo que se busque, y dónde se busque.

Mientras que la aceleración centrífuga (g_e, va hacia fuera la que nos expulsa del planeta) depende de la velocidad de giro y distancia al eje, y actúa siempre en contra del eje; la aceleración gravitatoria (g_r) disminuye a medida que nos acercamos al núcleo del planeta, y avanza en su dirección. Vamos, como en la Tierra, la aceleración gravitatoria va hacia abajo.

En otras palabras, la suma es sencilla pero no es para nada intuitiva. En función de la velocidad de giro elegida para el planeta (?₀) tendremos gravedades muy dispares en su interior, que dependerán de a qué distancia del centro nos encontremos (r) y nuestra latitud con respecto al ecuador (?):

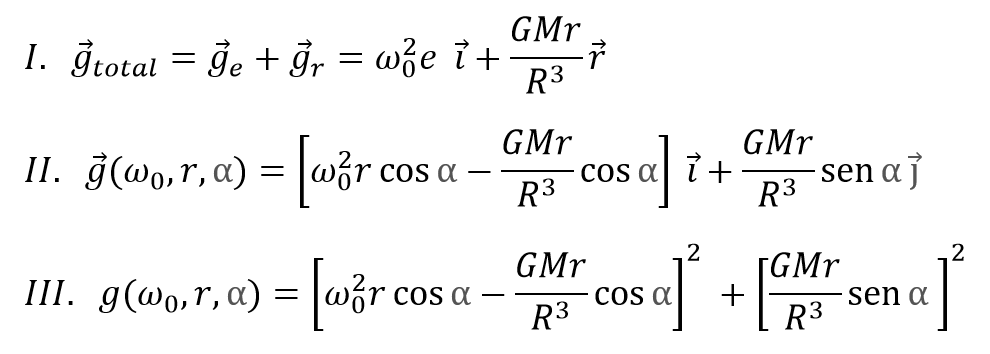
De nuevo, no te preocupes si las ecuaciones no te dicen nada. Es normal que no lo hagan.

Una manera de ver el problema es pensar en cuánta gravedad queremos en algún punto del planeta para así jugar con la posición (r y ?) y la velocidad del planeta (?₀) para conseguirla. Por ejemplo, si queremos una gravedad terrestre g₀, la encontraremos en los puntos que cumplan esta ecuación:

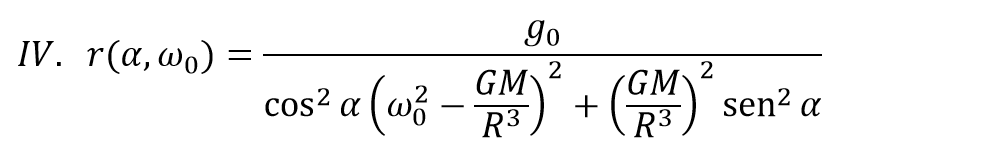
Lo sé, nada intuitiva y que nos dice entre muy poco y nada en absoluto. ¿Y si lo vemos con gráficas?

Si nos vamos al extremo de acelerar muy poco el planeta hasta conseguir en su interior una moderadísima gravedad de 0,28 m/s² (como en la superficie), podemos encontrar curvas curiosas que todavía dependen en gran medida de cuánta masa hay en el interior del planeta:

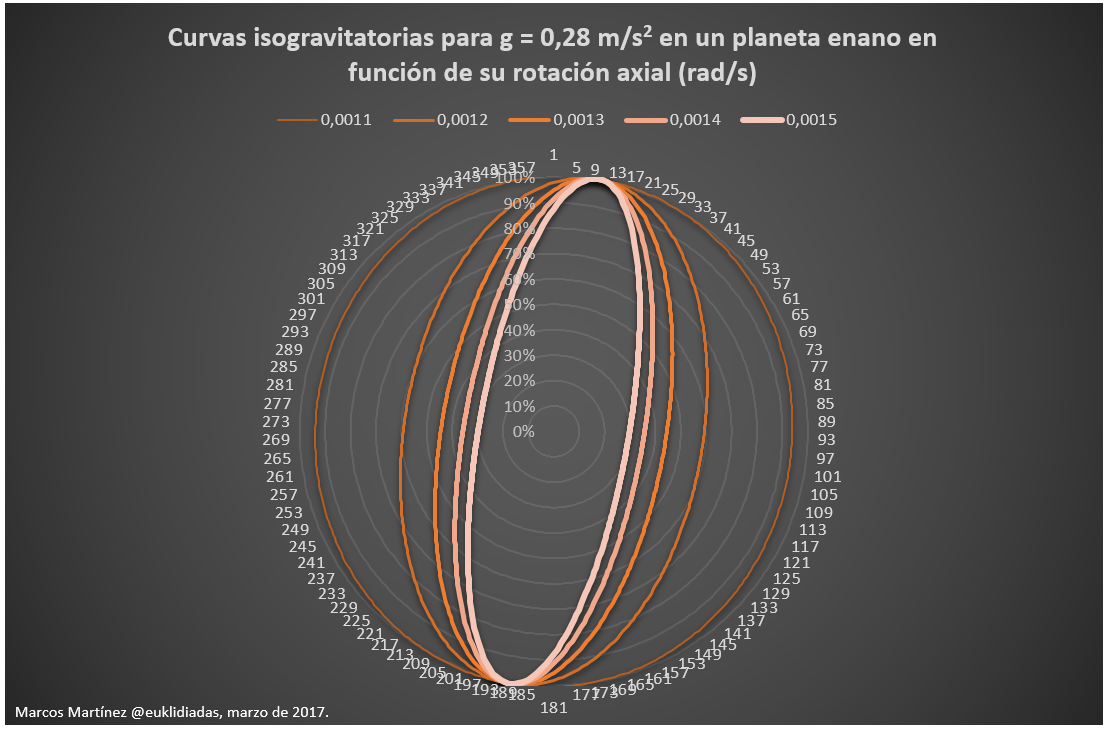
NOTA: En la imagen se ve un Ceres compuesto de números. El contorno son los grados medidos desde un punto cercano al eje de rotación actual, y el interior muestra (en porcentaje) la distancia al centro.

Todas las curvas de la imagen son lugares sobre los que los habitantes de Ceres podrían pasear (boca abajo) a baja gravedad en función de lo rápido que gire el planeta. Pero, si vas a pasar más de un fin de semana en Ceres, pide que lo aceleren algo más (por salud).

Conseguir números cercanos a 9,81 m/s² será algo poco realista debido al coste energético que eso supone pero, ¿a quién no le gustaría ver amanecer entre 28 y 39 veces a la hora? Eso lo que supondría para Ceres velocidades de giro del orden de los 0,005 a 0,007 rad/s.

Con estas velocidades, las líneas iso-gravitatorias (líneas sobre las que existe la misma gravedad en todos sus puntos) parecen casi rectas, y el componente de la gravedad que da la masa del planeta es casi despreciable:

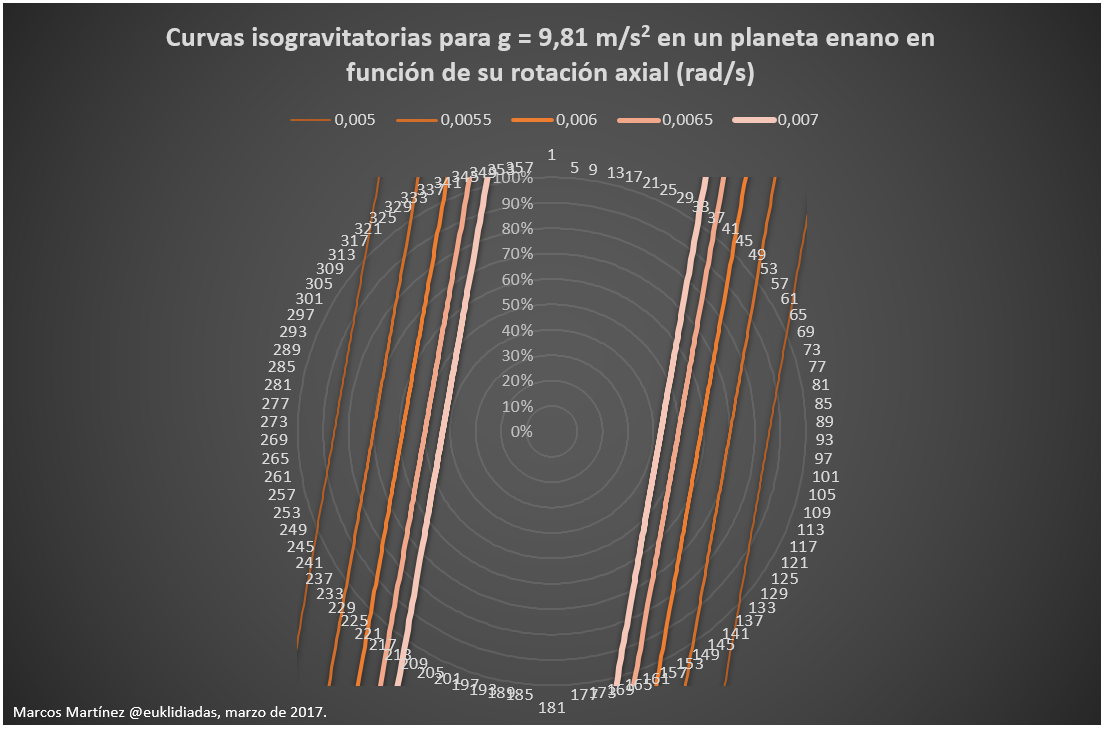
Es un diagrama menos bonito que el primero pero más fácil de trabajar. Aunque veamos solo líneas tenemos que pensar que Ceres está girando, y que esas líneas son en realidad gigantescos cilindros iso-gravitatorios. Una ingente cantidad de superficie con gravedades terrestres. Pero, ¿de cuántos kilómetros cuadrados?

¿Qué superficie se gana acelerando Ceres?

Como puede verse en la imagen de abajo con los distintos cilindros de colores extendidos, cada nivel iso-gravitatorio de un planeta en rotación genera una inmensa superficie:

Superficies iso-gravitatorias conseguidas en el interior de Ceres, desplegadas. Fuente: Marcos Martínez mediante Cinema 4D.

Imaginemos en un ejemplo que construimos un nivel en la superficie, y otro nivel cada kilómetro bajo el hielo de Ceres. Si existiese un nivel a 1 km bajo la línea del ecuador (similar al cilindro morado de la imagen), su área desenrollada daría más de 90.000 km². Un nivel a 2 km de la superficie, 130.000 km², y un tercer nivel cerca de 160.000 km². Hablamos de grandes números.

Con un Ceres girando a 0,0046 radianes (para tener cerca de estos niveles algo parecido a 9,81 m/s²) y construyendo niveles similares en tan solo los trece primeros kilómetros, el área acumulada daría como resultado una superficie de 2.950.000 km² (España entera tiene casi 506.000 km²).

Es decir, obtendríamos un poco más que el área total de Ceres sin apenas arañar la superficie. Y las diferencias de gravedad entre ellos serían muy bajas:

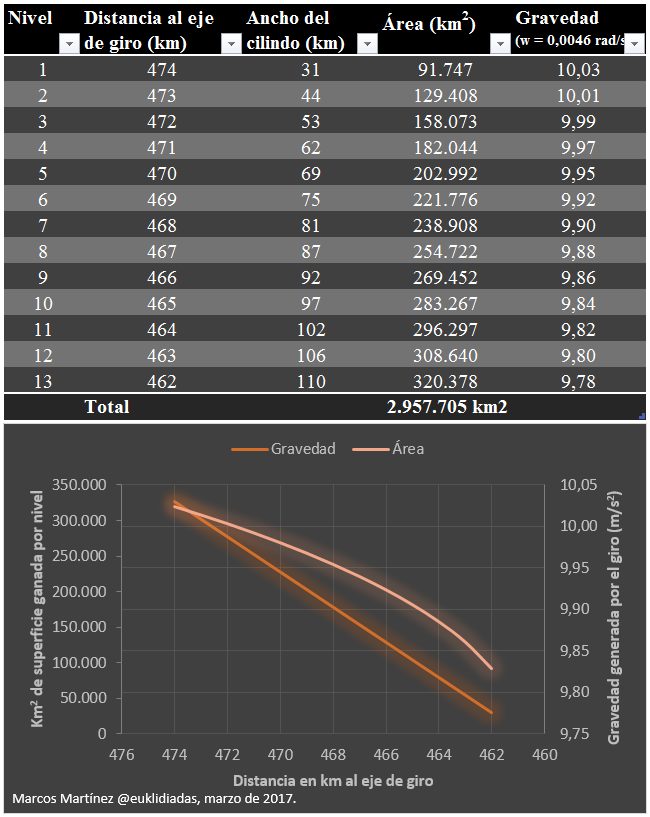
En The Expanse todos estos factores se tienen en cuenta a la hora de diseñar la estación. Además de otros que intervienen en la ecuación y que nada tienen que ver con los cálculos físicos.

A una solución ingenieril que distribuiría a la población en anillos concéntricos por el interior del planeta se le une la problemática propia de una colonia humana. En la serie, Ceres es el equivalente a las colonias americanas de España, Portugal e Inglaterra del s.XVII, por lo que para controlar a los cinturinos se diseñan estaciones más bien compactas.

De modo que se realiza una mezcla entre un Ceres aglutinado y un Ceres en base a anillos concéntricos abiertos, que es la que puede visualizarse en el panel del metro mencionado antes:

Otros factores a tener en cuenta

La serie The Expanse tiene también en cuenta factores como el Efecto Coriolis, que provoca que aparezca otra gravedad más porque un objeto (como un vagón de metro) avanza a cierta velocidad dentro de otro objeto girando (el planeta).

Aunque se aprecia no demasiado bien, efecto de la Fuerza de Coriolis en un vehículo en movimiento dentro de un Ceres en rotación. Fuente: The Expanse 1×01.

De ahí que los vagones del metro de Ceres se inclinen de un modo extraño cuando se ponen en marcha. Este mismo efecto ha sido mostrado por los guionistas a través de la caída libre de líquido en el interior del planeta enano, con comportamientos tan extraños para nosotros como este:

Efecto de curvatura que tienen los líquidos una vez empiezan a caer. Fuente: The Expanse 1×02. Aquí en movimiento.

Los guionistas de esta serie se han vuelto tan neuróticos y concienzudos con los cambios de gravedad asociados a las distintas aceleraciones en las diferentes escenas (Tierra, Marte, Ceres, Eros, naves espaciales en evasión o giro…) que las hojas del guion son de diferentes colores para que nadie se equivoque durante el rodaje.

Incluso se tienen en cuenta factores tan dispares como el modo que tienen las telas de oscilar en función de la distancia al centro del planeta enano; o sobre qué pierna se apoya más un personaje si avanza por los túneles en el sentido del giro de Ceres o en el sentido contrario. Nada queda al azar.

A la NASA le quedó claro ya en la primera temporada que si en el futuro queremos explorar el Sistema Solar exterior deberíamos tener presente los cálculos de series como The Expanse. Por su fidelidad a la hora de recrear los diferentes entornos. Cálculos incluyen hasta las modificaciones en el lenguaje de aquellos que partan de la Tierra para no volver.

En Nobbot | Un telescopio de la NASA descubre siete planetas donde buscar vida

Imágenes | NASA, Yakov Perelmán, Yakov Perelmán