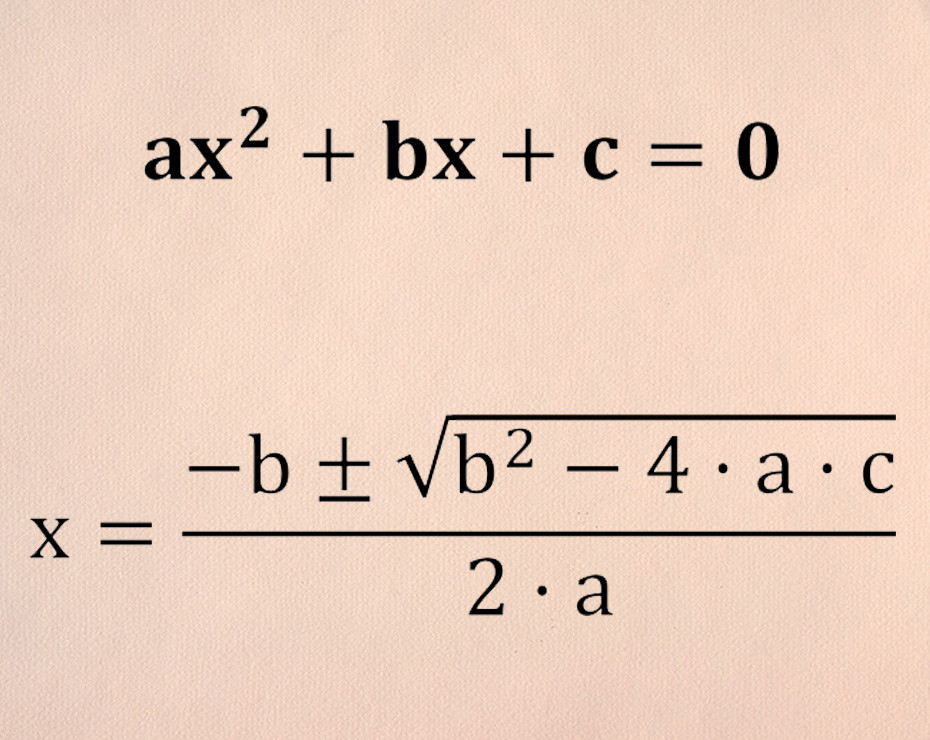Las ecuaciones de segundo grado son un tipo de ecuaciones que atascan a muchos alumnos. Mientras que las de primer grado son relativamente fáciles, hay un salto conceptual al llegar a las de orden dos.
Y otro mayor al pasar a las funciones cuadráticas, que podríamos decir que es el siguiente nivel. En este artículo aprenderás a identificar ecuaciones de segundo grado y a resolverlas.
Índice
- ¿Qué es una ecuación de segundo grado
- Tipos de ecuaciones de segundo grado
- Cómo resolver ecuaciones de segundo grado
- La factorización de la ecuación de segundo grado
¿Qué son las ecuaciones de segundo grado?
Una ecuación de segundo grado es una función en la que la única incógnita tiene como exponente el 2. Todas tienen la forma que vemos abajo, donde A, B y C son números naturales; y todas cumplen como condición que A ? 0:
Ax2 + Bx + C = 0 donde a ? 0
¿Por qué A no puede ser cero? Porque entonces quedaría una ecuación de tipo “Bx + C = 0”, que es una ecuación lineal. Las siguientes ecuaciones son ecuaciones de segundo grado, que mostramos primero en un orden aleatorio acompañadas de su tipo (Completas e Incompletas) y luego según el patrón que vemos arriba, al que se llega pasando todo a uno de los dos términos:
| Ecuación desordenada | Ecuación ordenada |
| x2 = 7(Incompleta) | x2 + 0x ? 7 = 0A = 1; B = 0; C = ? 7 |
| 3x2 = ? 2x(Incompleta) | 3x2 +2x + 0 = 0A = 3; B = 2; C = 0 |
| 2x2 + 3x = 2(Completa) | 2x2 + 3x ? 2 = 0A = 2; B = 3; C = ? 2 |
| x2 +5x ? 24 = 0(Completa) | x2 +5x ? 24 = 0A = 1; B = 5; C = ? 24 |
| ?x2 = 1x(Incompleta) | x2 + x + 0 = 0A = 1; B = 1; C = 0 |
Tipos de ecuaciones de segundo grados
Aunque todas las ecuaciones de segundo grado siguen la fórmula de arriba, podemos diferenciarlas en dos tipos:
- Ecuaciones de segundo grado completas. En ellas se cumple que B ? 0 y que C ? 0.
- Ecuaciones de segundo grado incompletas. En ellas al menos uno de sus coeficientes B o C es igual a 0. Puede ser que B = C = 0.
¿Cómo resolver ecuaciones de segundo grado?
Hay una fórmula maestra para resolver todas las ecuaciones de segundo grado. Lo único que hay que hacer es preparar la ecuación para verla según la fórmula general “Ax2 + Bx + C = 0” y luego aplicar la fórmula de abajo. Vamos a verlo a través de los tres primeros ejemplos de arriba.
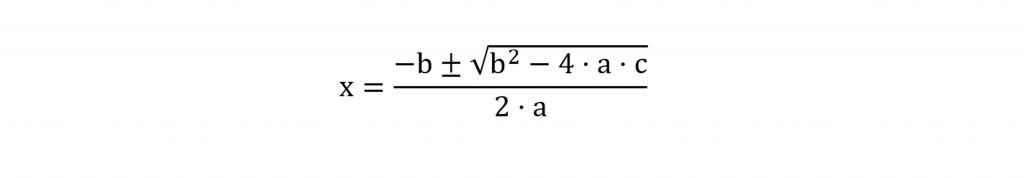
Ejemplo 1. x2 = 7
Paso 1. Llevamos al primer término todos los elementos:
x2 ? 7 = 0
Paso 2. Identificamos A, B y C. Estos números pueden encontrarse también como a, b y c en los libros, e incluso con otras letras como u, v y w. Aquí los escribimos con mayúscula para que se vean bien.
A = 1; B = 0 (porque no hay x); C = ? 7
Paso 3. Aplicamos la fórmula maestra y operamos. A partir del igual rojo, hemos factorizado el contenido de la raíz, sacando fuera todos aquellos números elevados a 2. Es posible que aún no lo hayamos dado en clase, en cuyo caso la solución es mucho menos elegante.
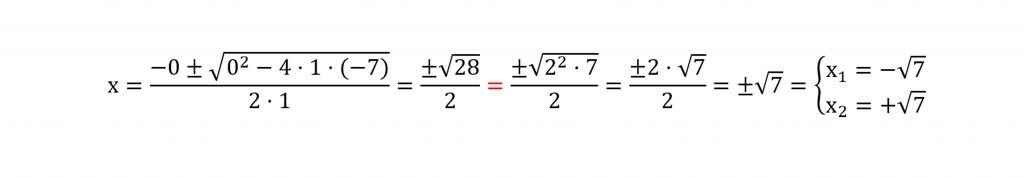
Las soluciones de este ejercicio, a las que se llaman raíces, son ??7 y ?7.
Ejemplo 2. 3x2 = ? 2x
Paso 1. Llevamos al primer término todos los elementos:
3x2 + 2x = 0
Paso 2. Identificamos A, B y C:
A = 3; B = 2; C = 0
Paso 3. Aplicamos la fórmula maestra y operamos. Como puedes ver, ninguno de estos ejemplos tiene una solución entera. Es importante acostumbrarse a soluciones poco estéticas, y a simplificarlas, como es el caso:
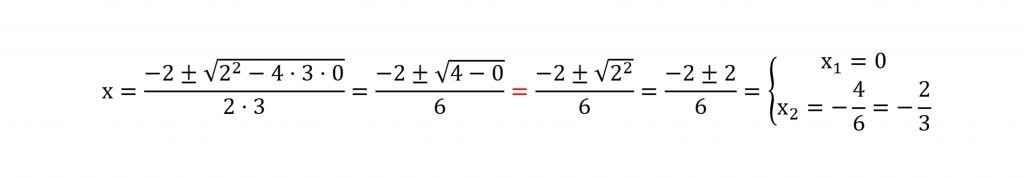
Ejemplo 3. 2x2 + 3x = 2
Paso 1. Llevamos al primer término todos los elementos:
2x2 + 3x ? 2 = 0
Paso 2. Identificamos A, B y C:
A = 2; B = 3; C = ? 2
Paso 3. Aplicamos la fórmula maestra y operamos.
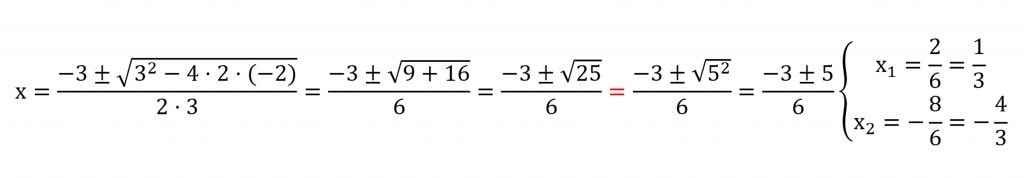
La factorización de la ecuación de segundo grado
Los factores son cada uno de los elementos de una multiplicación. Así, “2 x 3 = 6” es una operación de multiplicación en la que “2” y “3” son los factores de “6”. Del mismo modo, las ecuaciones de segundo grado tienen factores, que guardan relación con sus soluciones o raíces. De hecho, los factores tienen esta forma:
(x ? x1)·(x ? x2) = 0
“x ? x1” es el primer factor y “x ? x2” es el segundo factor. ¿De dónde sacamos x1 y x2? Lo cierto es que ya lo hicimos arriba. Son las raíces que ya calculamos. Aun así, podemos obtener estas soluciones por el método de factorización, que explicamos con los últimos dos ejemplos.
Ejemplo 4. x2 +5x ? 24 = 0
En este caso, el primer paso ya lo tenemos porque tenemos la ecuación según la expresión general, con todos los elementos en el primer término. Ahora buscamos dos números que, multiplicados, den C; y sumados den B. Es decir, que cumplan:
x1·x2 = C = ? 24
x1 + x2 = B = 5
En este caso, ?8 y 3 son dos números que cumplen estas condiciones, por lo que las raíces serán:
(x +8)·(x ? 3) = 0
Pero ocurre que este método puede ser bastante complicado si los factores son difíciles, como han sido los ejemplos 1, 2 o 3. No es recomendable usarlo a menos que tengamos mucha soltura matemática o el ejercicio sea muy fácil, como es el caso del ejemplo 5.
Ejemplo 5. ?x2 = 1x
Paso 1. Llevamos al primer término todos los elementos:
?x2 ? x = 0
Paso 2. Buscamos los números que cumplan:
x1·x2 = 0
x1 + x2 = ? 1
En este caso lo tenemos mucho más fácil que antes porque si la multiplicación de las raíces da 0 es que al menos una de ellas es 0. Y si x1 es 0, entonces x2 es ? 1. De modo que la factorización se ve así:
(x ? 0)·(x + 1) = 0
Si nos fijamos, en este caso podríamos haberlo resuelto de una forma aún más sencilla sacando factor común a la x en la primera ecuación:
?x2 ? x = 0
x·(?x ? 1) = 0
x·(x + 1) = 0
(x + 0)·(x + 1) = 0
Aunque no hay una única forma de resolver una ecuación de segundo grado, la fórmula maestra funciona siempre, y se recomienda su uso.
Imágenes | Propias