Pocos países se han adelantado al comportamiento exponencial de la pandemia de la COVID-19. ¿Por qué? Considerándola, en principio, algo leve, a muchos les ha costado doblegar la curva y la mayoría de naciones tienen rebrotes de dimensiones importantes. Probablemente se debe a que a los humanos se nos da muy mal pensar de forma exponencial, como demuestran estos problemas:
- Problema 1. «Una persona está atrapada en un barril casi vacío en el que cada minuto se duplica el agua del interior. Tras una hora, el barril está lleno. ¿En qué minuto el agua del barril estaba a la mitad de la altura y se podía respirar?”.
- Problema 2. “Una persona vende un tablero de ajedrez por granos de arroz, siguiendo una regla: en cada casilla el comprador pondrá el doble de granos de arroz que en la anterior, empezando por uno. ¿Es un buen trato?”.
Las soluciones, más abajo. Pero antes vamos a ver por qué una pandemia se comporta de forma exponencial.
R0>1 implica pandemia exponencial
La tasa de contagio R0 es una simplificación matemática que ayuda a entender cómo se extiende una pandemia. Indica a cuántas personas infecta cada contagiado. Una enfermedad con R0=2 implica que cada contagiado infecta a dos personas; con R0=3, a tres.
A finales de mayo, las medidas de distanciamiento social y la mascarilla en España lograron que el R0 fuese de 0,3. Sin embargo, la curva volvía a crecer hacia el 8 de junio. ¿Por qué pasa esto? Porque el R0 no es estático. En un aislamiento perfecto sería de 0; sin ninguna medida estaría entre 1,4 y 5,7.
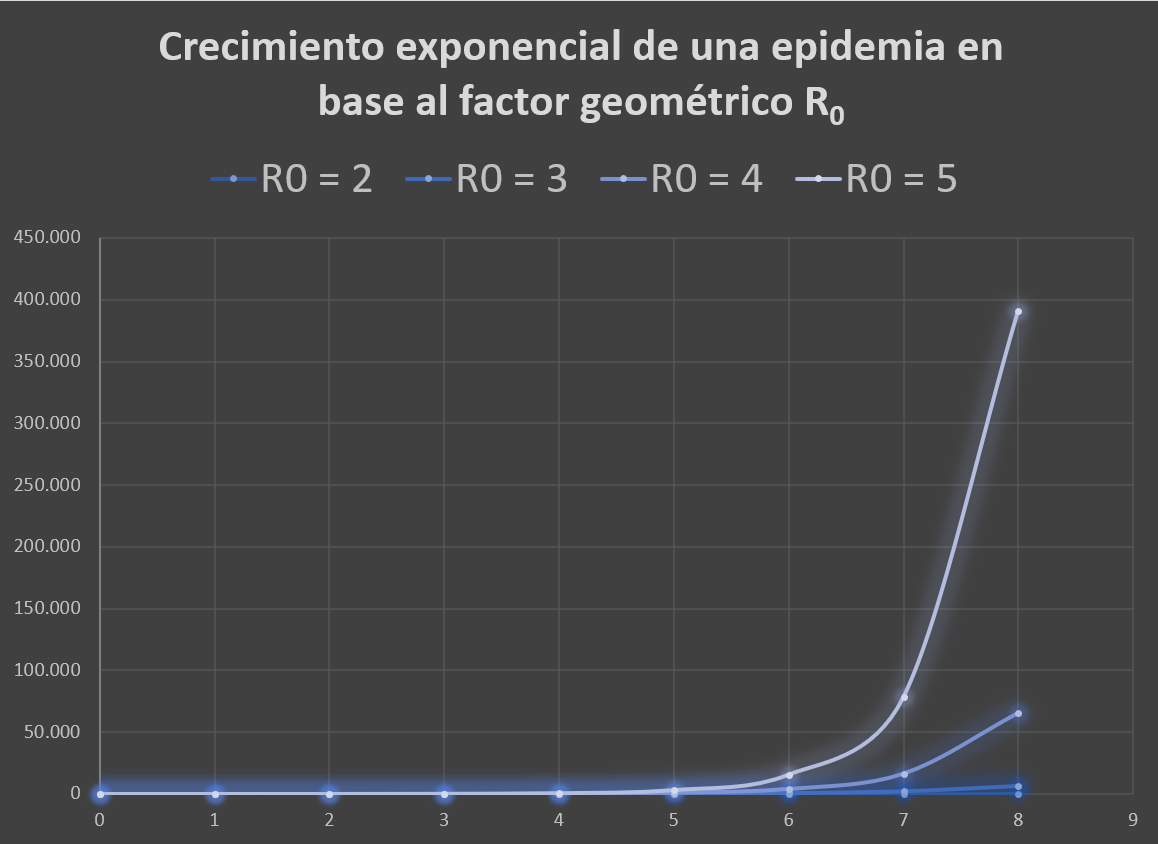
La gráfica de arriba muestra cuatro pandemias diferentes basándose en su R0 y ejemplifica el serio problema que se presenta para anticipar comportamientos exponenciales. Hasta la cuarta semana las tres pandemias tenían un comportamiento ‘similar’ y casi plano. Un mes después, la que tiene un R0 de 5 es una catástrofe que ha saturado la sanidad.
En este escenario, en solo cuatro semanas la situación se ha ido completamente de las manos y cualquier medida seguirá siendo necesaria, pero habrá llegado tarde. ¿Es posible reaccionar cuando ‘solo’ hay unos pocos infectados? Los datos agregados de los países muestran que todos parecen subestimar los contagios cuando estos se reducen.
el barril que se llena de agua
- Problema 1. “Una persona está atrapada en un barril casi vacío en el que cada minuto se duplica el agua del interior. Tras una hora, el barril está lleno. ¿En qué minuto el agua del barril estaba a la mitad de la altura y se podía respirar?”.
Antes de dar la solución realizaremos un pequeño cálculo basado en el mismo problema. ¿Y si al inicio del problema hubiese una gota en el fondo del barril? Al terminar el primer minuto habría dos. Tras el segundo, cuatro; al final del cuarto, ocho, etcétera. ¿Y al final del minuto 60?
Pues habría 1,15 millones de millones de millones de millones de gotas. Exactamente 1.152.921.504.606.850.000 de gotas, el equivalente a 125 piscinas olímpicas repletas de agua hasta arriba. De modo que es evidente que nuestro barril solo contenía unas pocas moléculas de agua al inicio del problema.
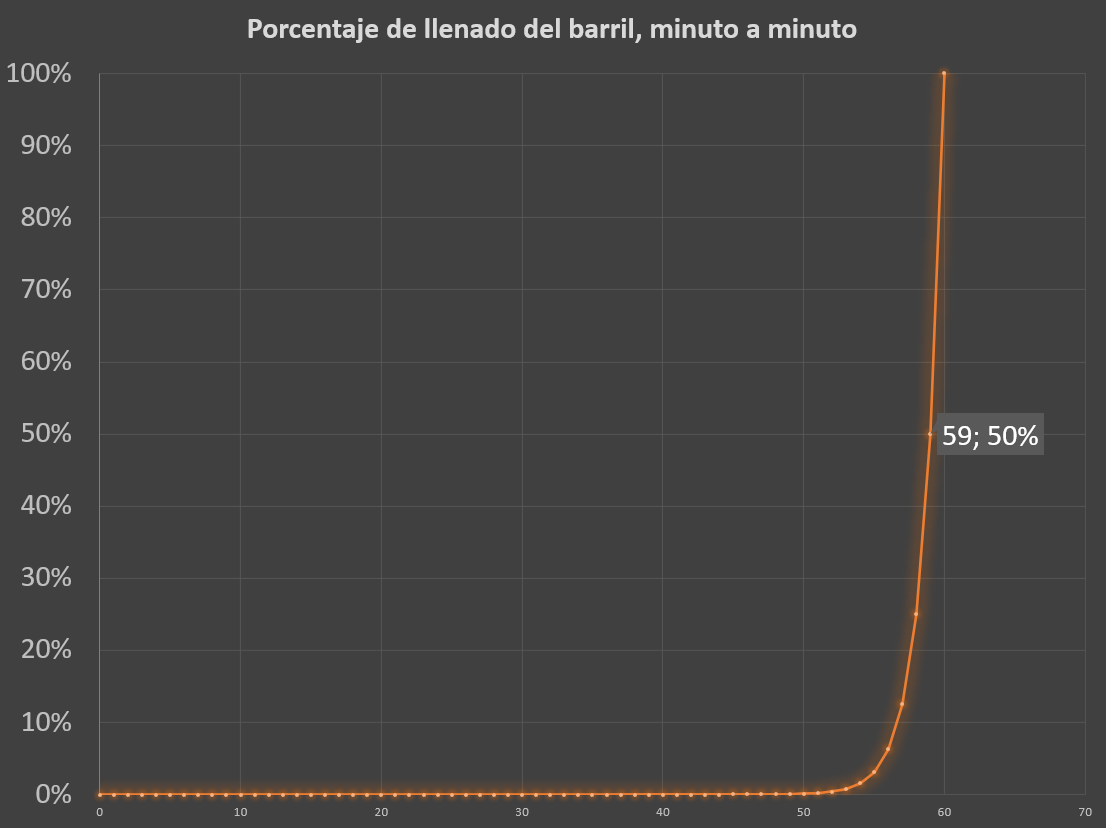
Y he aquí la respuesta al primer problema. Como podemos ver en el gráfico, el barril tarda 59 minutos en llenarse hasta la mitad. De hecho, hasta el minuto 53 no alcanza el 1%. Sin embargo, durante el último minuto el agua cubre rápidamente al ocupante del barril, un comportamiento que muchos no habrán sido capaces de predecir.
La venta del ajedrez por arroz
- Problema 2. “Una persona vende un tablero de ajedrez por granos de arroz, siguiendo una regla: en cada casilla el comprador pondrá el doble de granos de arroz que en la anterior, empezando por uno. ¿Es un buen trato?”.
Este problema cuenta con siglos de antigüedad y se relaciona con la cultura brahmánica. Si uno no entiende la mecánica del crecimiento exponencial, podría caer en el error de pensar que es un ajedrez barato, sin darse cuenta de que cuesta 18.446.744.073.709.551.615 granos.
¿Cuánto es eso? Pues unas 838.488.366.986 toneladas de arroz. En 2017 la FAO estimó que durante 2018 se alcanzarían los 769,9 millones de toneladas en todo el mundo, mil veces menos. Este ajedrez cuesta casi toda la producción de toda la década de 2020. De modo que no, no es un buen trato para el comprador, es un engaño matemático.

¿Cómo analizamos comportamientos exponenciales?
Los seres humanos no han evolucionado para pensar de forma geométrica o exponencial; tampoco para defenderse de tigres de cuatro dimensiones. Si uno abre sus fauces bajo sus pies, se los comerá seguro. No solo no podemos pensar en 4D, sino que ni siquiera dispondríamos de receptores sensoriales preparados para ellos. Y una pandemia exponencial funciona en una suerte de 4D.
Nuestra mente piensa de forma lineal y le cuesta mucho contextualizar objetos que aceleran porque durante millones de años nada ha acelerado a nuestro alrededor. Los tigres, por mucho que corran, tienen una velocidad límite máxima. Y si uno corre más, los esquiva. Para la COVID-19 hay que ser más listos.
Saber cómo afecta la velocidad a la distancia de frenado, entender el problema del calentamiento global o intentar predecir pandemias es prácticamente imposible sin herramientas matemáticas avanzadas. Y ahí está la clave: matemáticas y modelos computacionales.
La ciencia y los modelos predictivos son los únicos que puede alertar de pandemias que están por venir y, en realidad, no son tan difíciles de comprender una vez se han conceptualizado y dibujado en gráficas como las de arriba. Todos entendemos ahora cómo se aplana la curva del coronavirus y lo que son las R0.
Algunas herramientas básicas para una buena detección son apps que diagnostican con la tos, procesos con radiografías de rayos-X que funcionan en minutos o el análisis de aguas residuales. Una vez hecha esta detección es posible construir un modelo matemático de aviso. Pero hay que saber confiar en estos algoritmos.
En Nobbot | Pos-COVID-19: Nadie tiene una bola de cristal pero existen el método científico y el sentido común
Imágenes | iStock/BiancaGrueneberg, iStock/Maren Winter