La transformada de Fourier es una operación matemática indispensable para un gran número de disciplinas. Se usa en campos como la medicina, las telecomunicaciones, la ingeniería acústica, los circuitos eléctricos, el diseño de puentes frente a resonancias y la compresión de pistas de audio, entre otros.
Esta transformada se consigue aplicando una fórmula matemática a una función. Aunque esta fórmula es matemática ‘avanzada’. Requiere el nivel de segundo de bachillerato y exige saber resolver integrales y comprender funciones complejas en forma polar.
¿Qué es la transformada de Fourier?
La transformada de Fourier es una transformación matemática usada para transformar señales entre el dominio del tiempo o espacio al dominio de la frecuencia, y viceversa. El concepto de ‘transformada de Fourier’ se refiere a varios conceptos de forma simultánea:
- Operación de transformación de una función.
- Función resultado de la operación.
- Espectro de frecuencias de una función.
La función original suele recibir el nombre de x(t), siendo muy común que ‘t’ sea el tiempo, mientras que la función transformada suele recibir el nombre de X(f), en mayúscula, siendo ‘f’ la frecuencia.
Como ejemplo, si se tiene una función p(t) donde ‘p’ es la potencia de una señal acústica y t el tiempo, P(f) es una transformada de Fourier que informa de cómo se distribuye p(t) en función de la frecuencia la potencia de la señal.
En otro ejemplo, si e(s) informa sobre la energía de una señal en función del espacio, E(f) es una transformada de Fourier que informa sobre cómo se distribuye e(s) en función de la frecuencia de la energía de la señal.
Es importante destacar que aunque el tiempo, el espacio y la frecuencia son valores reales, tanto x(t) y x(s) como sus respectivas transformadas X(f) no tienen por qué tomar valores reales. En los ejemplos de potencia y energía es posible que las magnitudes tengan elementos complejos.
¿Cuál es una frecuencia de una función no periódica?
Si e(t) es una función periódica (función que se repite), es fácil pensar en los conceptos inversos ‘frecuencia’ y ‘periodo’. Aunque a menudo surge la duda de cuál puede ser la frecuencia de una señal no periódica. ¿Qué frecuencia tienen x(t) = 1 o e(s) = ?x + 1?
El concepto de frecuencia de la transformada de Fourier no tiene por qué guardar relación con la inversa del periodo de la función original, sino con la brusquedad o rapidez de los cambios en los valores de x(t) o e(s).
¿Cómo se calcula la transformada de Fourier?
A pesar de que calcular la transformada de Fourier de una función es bastante sencillo, es necesario aprender a integrar múltiplos de funciones complejas con anterioridad. Si x(t) es la función original, su transformada X(f) será:
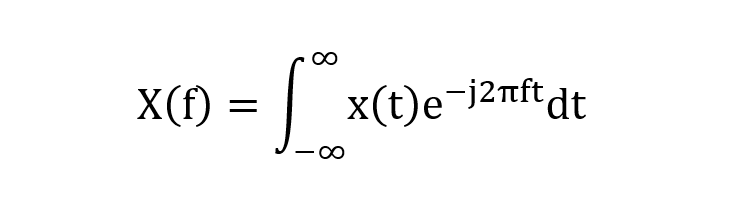
Para obtener la transformada es importante tener presente varios puntos importantes:
- La integral actúa sobre ‘t’ (‘s’, si la función original depende del espacio), de modo que la frecuencia ‘f’ debe ser tratada como si fuese una constante. De hecho, el exponente ‘-j2?f’ es una constante.
- Si la función original existe entre dos valores reales a y b, la primitiva de la integral se resuelve entre esos valores reales.
¿En qué funciones puede aplicarse la transformada de Fourier?
En principio, para que una función pueda transformarse mediante la operación de Fourier ha de cumplir varias condiciones conocidas como Condiciones de Dirichlet. A saber:
- Condiciones débiles de Dirichlet. Los coeficientes de fourier deben ser finitos. Dicho de otra forma, la función de partida ha de ser absolutamente integrable.
- Condición 1. La integral entre dos puntos cualesquiera del módulo de la función de partida ha de ser menor que infinito:
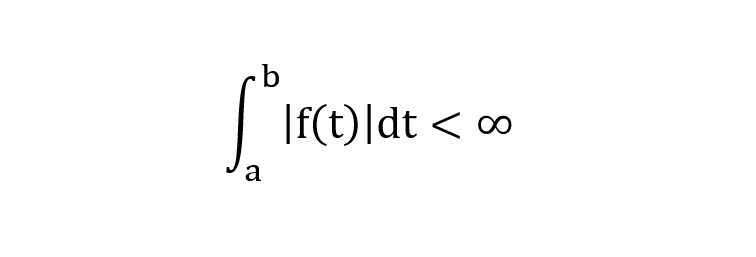
- Condición 2. la integral de menos infinito a infinito del módulo de la función ha de obtener un resultado menor que infinito:
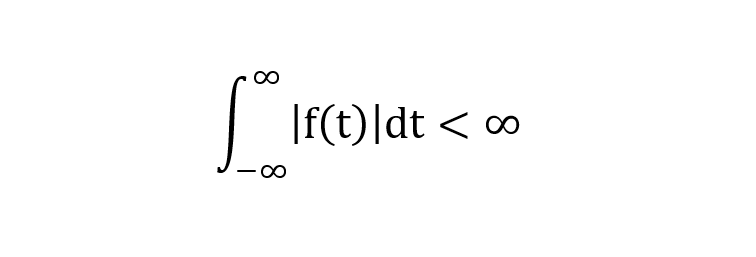
- Condiciones fuertes de Dirichlet. En cualquier intervalo finito, la función de partida tiene:
- Un número finito de discontinuidades finitas.
- Un número finito de máximos y un número finito de mínimos.
¿Para qué sirve la transformada de Fourier?
Dejando a un lado el tema matemático, la transformada de Fourier tiene muchas aplicaciones en ingeniería, medicina o telecomunicaciones. Uno de los ejemplos más usados es la transformación de señales de potencia y energía de cara al envío de información por cables u ondas. Esta transformación permite la ocupación de todo el espectro radioeléctrico.
En acústica, las transformadas de Fourier tienen diferentes usos, desde comprimir audio a limpiar el ruido de archivos. La compresión de archivos usando este tipo de fórmulas también se usa en archivos como imágenes o vídeos; no tiene por qué ser de audio.
En ingeniería civil es frecuente el uso de estas transformadas para calcular el comportamiento de grandes estructuras, como puentes, ante fuerzas de alta energía como el viento. Además, en los últimos años ha surgido una nueva aplicación: el reconocimiento de voz, una tecnología que abre las puertas a la identificación biométrica por sonido.
En Nobbot | 10 maneras de aprender matemáticas sin tocar un libro
Imágenes | iStock/your_photo