Una de las asignaturas que menos simpatía despierta en el colegio, pero aun así hay que estudiar, son las matemáticas. Si ahora te preguntan por los triángulos rectángulos, ¿qué podrías decir acerca de esta figura geométrica? ¿Te ves capaz de calcular su área?
Índice
- Definición, elementos y propiedades del triángulo rectángulo
- Cómo calcular el área de un triángulo rectángulo y más fórmulas
- Ejemplos resueltos de problemas de triángulos rectángulos
Definición, elementos y propiedades del triángulo RECTÁNGULO
El área de conocimiento de las matemáticas es amplísimo. Así, una de las partes que la conforman es la geometría, una rama que estudia las propiedades que tienen las figuras en el espacio y sobre el plano. Una de estas figuras son los triángulos rectángulos y la característica que les distingue de otras formas geométricas es que poseen un ángulo interior recto de 90º.
Elementos principales de un triángulo rectángulo
Los elementos más importantes de un triángulo rectángulo son los siguientes:
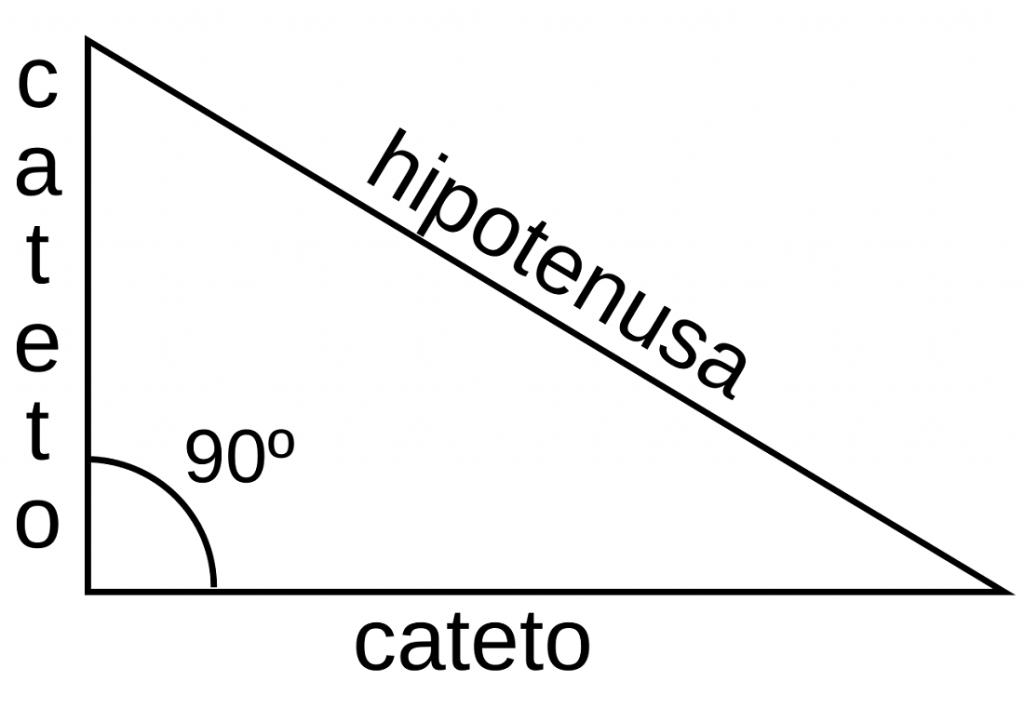
- Hipotenusa: es el lado de mayor longitud del triángulo que está opuesto al ángulo recto.
- Catetos: son los lados del triángulo que forman el ángulo recto.
- Ángulo recto: ángulo de 90º que forman los dos catetos.
- Ángulo agudo: el triángulo rectángulo tiene dos ángulos agudos menores de 90º. Al sumarlos, el valor que se obtiene son 90º.
Tipos de triángulo rectángulo
Dado que la longitud de sus lados no siempre es la misma, se establece una doble clasificación:
- Triángulo rectángulo escaleno: sus tres lados son diferentes y sus ángulos también, a excepción del que mide 90º.
- Triángulo rectángulo isósceles: en este tipo de triángulo rectángulo, los catetos miden lo mismo y, por lo tanto, sus ángulos interiores también: 45º.
Propiedades del triángulo rectángulo
Al igual que sucede con otras figuras y cuerpos geométricos, los triángulos rectángulos poseen diferentes propiedades. Una de las más conocidas está relacionada con el Teorema de Pitágoras. Dice lo siguiente: el cuadrado de la hipotenusa (es decir, el lado opuesto al ángulo recto del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos. El filósofo y matemático griego Pitágoras ya comprobó esta relación matemática en el siglo VI a. C., de ahí que el teorema haya tomado su nombre del aclamado pensador matemático. Otra de sus particularidades es que el lado de la hipotenusa siempre es mayor que cualquiera de los dos catetos.
Cómo calcular el área de un triángulo rectángulo y más fórmulas
A continuación, vamos a explicar cómo se puede calcular el área de un triángulo rectángulo y otras fórmulas como el perímetro y la altura.
Área
Se calcula multiplicando la base (a) por la altura (h). Luego, el resultado de esta operación se divide entre dos. De forma matemática se representa así: a x h / 2.
Imaginemos un triángulo rectángulo que tenga de base 15 y de altura 8. Su área se calcula del siguiente modo: 15 x 8 / 2 = 60.
Perímetro
La fórmula más sencilla de calcularlo, siempre y cuando conozcamos cuánto mide la hipotenusa y los dos catetos, es la siguiente: perímetro = a la suma de los tres lados. ¿Qué sucede si, por ejemplo, se desconoce cuánto mide la hipotenusa? En este caso, hay que tener en cuenta el Teorema de Pitágoras, porque gracias a él es posible saber cuánto mide la hipotenusa (C) a partir de los catetos (A y B). La fórmula que hay que resolver es: perímetro = A + B + ? A² + B².
Imaginemos que tenemos un triángulo rectángulo. El cateto A mide 7 y el cateto B 12.
- Lo primero es sumar 7 más 12, que son 19.
- A continuación, calculamos el cuadrado de A (según el ejemplo, 49) y el de B (144) y sumamos sus cifras (193).
- Llegados a este punto, hay que calcular la raíz cuadradada de 193 (13,89).
- A su resultado, hay que sumarle 19 (la primera de las operaciones realizadas (13,89 + 19 = 32,89).
- Como el perímetro de un triángulo rectángulo se obtiene sumando cada uno de sus tres lados, y ya conocemos que el lado de la hipotenusa mide 32,89, resolveríamos de la siguiente manera: 32,89 (lado de la hipotenusa) + 12 (cateto A) + 7 (cateto B) = 51,89.
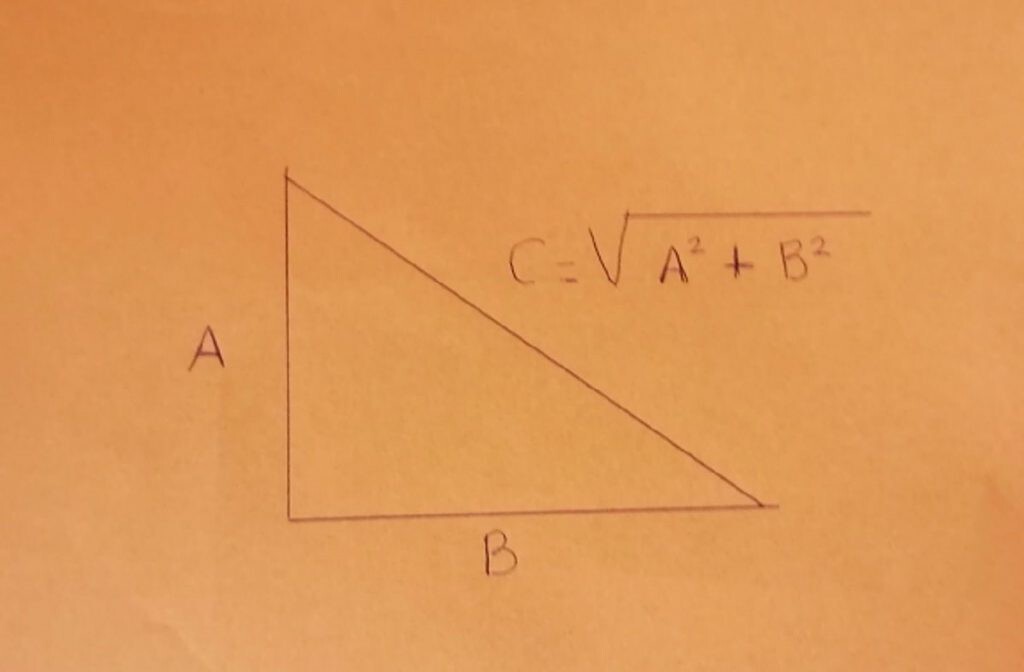
Altura
Para calcular este valor, hay que basarse nuevamente en el Teorema de Pitágoras, que recordemos que dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Es decir, C² = A² + B².
Vamos a tomar como ejemplo un triángulo rectángulo que tiene como base (A) 6 e hipotenusa 12 (C)
- Para ‘despejar’ B de la fórmula se hace así: C² – A² = B².
- A continuación, se ‘deshace’ el cuadrado de B (recordamos que es la hipotenusa) y pasa al otro lado en forma de raíz cuadrada. La fórmula matemática queda resuelta del siguiente modo: ? (C² – A²) = B.
- ? (12² – 6²) = ? (144 – 36) = ?108 =10,39
En el ejemplo que hemos desarrollado, un triángulo rectángulo con una base 6 y una hipotenusa 12 tiene una altura de 10,39.
Ejemplos resueltos de problemas de triángulos rectángulos
Una vez hemos identificado las partes o elementos más característicos de esta figura geométrica y aprendido a calcular su área, altura y perimetro, resolveremos el siguiente problema.
¿Cómo calcular la altura de un triángulo rectángulo si conocemos su área?
- Recordemos que el área se calcula aplicando la fórmula de base (a) x altura (h) dividida entre dos, es decir: Área = a x h / 2.
- Ahora, hay que ‘despejar’ el 2 de la división y ‘llevarlo’ al otro lado para que quede así: Área x 2 = a x h.
- Una vez hecho, la base (a) que se está multiplicando por la altura (h) pasa a dividir de la siguiente manera: (Área x 2)/a = h
Imaginemos que tenemos un triángulo rectángulo cuya área mide 160 y la base (A) 50. Si aplicamos la anterior fórmula obtendremos directamente la altura (h) que es 6,4. (160×2)/50 = h.
Si quieres practicar diferentes problemas, puedes hacerlo desde este enlace.
En Nobbot | Parece sencillo, pero no lo es: cómo calcular el área de un triángulo
Imágenes | Vlado Paunovic/Pexels, KES47/Wikimedia Commons, captura propia